High dimensional array is a lot of pain

I was really struggling to understand high dimensional array, especially in all the operations that involves manipulation in the axes of these ndarrays.

If I could start all over again in learning Deep Learning, I would spend more time in understanding how to play around the dimensions in matrix, before rushing to build my first model. It has been a painful experience to do operations on tensors without clearly what the dimensions of the data.

If you are also struggling, I hope this article can provide some help to you.

TL;DR

• You should see High dimensional array (a.k.a ND-array) in collection of arrays
• The shape of the numpy array can be deceiving. A 2D object can have 3 dimensions (e.g. coloured image)
• Hence, having a mental model to match the ndarray to the actual object you want to represent is very important. For example, for a 2D image you should think about which part of the array represents the image dimensions.
• As Numpy is the foundation of Deep Learning Libraries such as PyTorch and Tensorflow, I will use numpy syntax to illustrate the idea. The same idea follows for those DL libraries.

What are dimensions?

In computer, there are many ways to store data. Data can be stored in a scalar format, an array format, a matrix (2D array) format, so on and so forth. These different format have different dimensions. In a very simplified way:

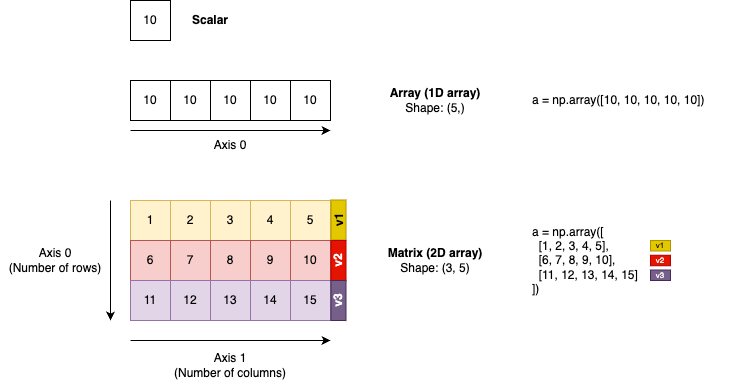
• Scalar: 0 Dimension. It stores one value in the memory. There is no length.
• Array: 1-Dimensional variable. It stores a number of values into a continuous block of memory. Array is also called “Vector” in some programming languages (e.g. R)
• Matrix: 2-Dimensional. Matrix is a collection of Arrays. It has rows and columns. In NumPy, it is better referred as 2D array

Although it is common to use mathematical terminologies, such as using scalar to refer to 0-D array, vector to refer to 1-D array, or matrix to refer to 2-D array, I think it is more clear to use the term “N”-Dimensional array to describe this NumPy component. It can reduce ambiguity and it also helps to think how the data is being structured in the memory.

Understanding N-Dimensional Array

In general, a “N”-Dimensional array is a collection of “N-1”-Dimensional array. Let me try to illustrate this point.

For a 2D-array, it is basically a collection of 1D-array. As you can see from below illustration, a 2D-array wish shape (3, 5) is a collection of 3 1D-array of shape (5,)

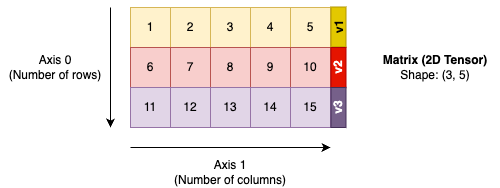
• In the above 2D-array, it is a collection of 3 arrays (v1, v2, v3), and these arrays are with the same shape (5,)
• The above 2D array will have a shape of (3, 5)

How about 3D arrays?

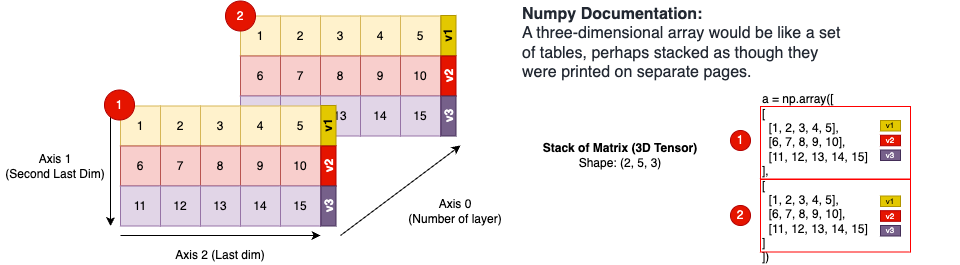
• In the above 3D arrays, it is a collection of 2 2D-arrays (The 2 tables that we highlighted in red)
• The above 3D array have a shape of (2, 3, 5)

However, when it is extended to 3D array, or even a higher dimensional, it is important to consider column is the last dimension and row is the second last dimension. This means when we should read the shape from right to left.

How to read the shape tuple value?

A shape of an N-Dimensional array should be read from right to left.

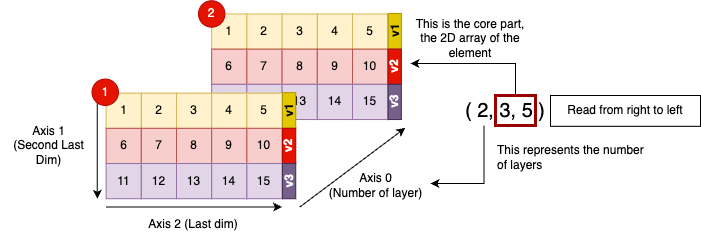
1. The rightmost part is the “core” part, which is the 2D array component. The n^th and (n-1)^th dimension represents the dimension of the 2D array
2. The next dimension to the left represents the number of layers of 3D-array.

This is also documented in the official NumPy tutorial:

It is familiar practice in mathematics to refer to elements of a matrix by the row index first and the column index second. This happens to be true for two-dimensional arrays, but a better mental model is to think of the column index as coming last and the row index as second to last. This generalizes to arrays with any number of dimensions.

Reference: https://numpy.org/devdocs/user/absolute_beginners.html

A “2-Dimensional object” can also represented by 3-Dimensional array

It may seem a bit odd to say that, but an object with 3 dimensions does not necessarily mean it is a “3D” object. This is why it is better to think dimensions in the way of “A collection of arrays”.

Let’s take the same example as above. Assume we have an object with shape (2, 3, 5). We can still represent it in a 2D object with 2 rows and 3 columns.

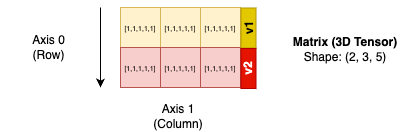
Yes, we can do that as long as we compress the last dimension into a matrix. In short, we are having a matrix of 2 rows and 3 columns, but the elements is an array with 5 elements. Does it look odd? May be. Yet, we use this every day.

Example – Representing a colour image

A 2D-array with a 3-element array is how we represents a colour image in data. An image contains height and width, and for each of the pixel it has 3 colour channels: R (Red), G (Green), and B (Blue).

In python, we can use the cv2 library to read an image and represent in numpy array.

import cv2, matplotlib.pyplot as plt

img = cv2.imread('idol.jpeg')

# When we import the image the default colour channel 
# is BGR. We have to flip it to become RGB. 
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)

plt.imshow(img)

Here, we can see the shape of the image is (270, 216, 3).

• The first axis represents the height, which is 270 px
• The second axis represents the width, which is 216px
• The third axis represents the colour channel, which is 3 (RGB)

If we subset a part of an image, as shown above, for each element in the 2D image, there is an array of 3 values that represents R (Red), G (Green), and B (Blue) channels, with values between 0 and 255.

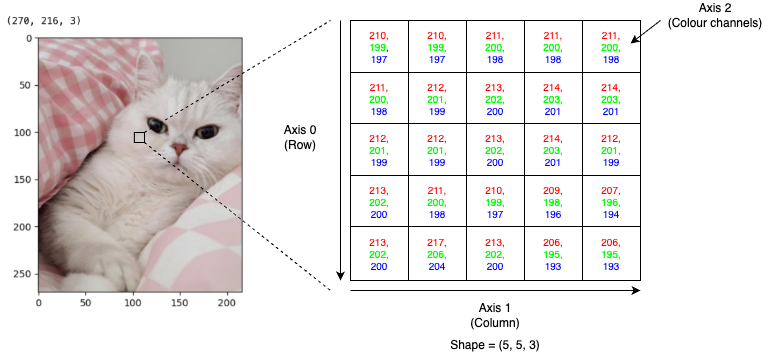
I hope this shows why it is better to think N-D array is a collection of arrays, but not to think it as a cube or something equivalent.

It is easier to think ND-array as a collection of arrays, instead of a vector, or a cube, or even higher dimensional tensor.

Conclusion

Understanding ND-array is important because there are a lot of operations will be done on these data. These operations are the foundation of Deep Learning.

A key takeaway is when dealing with high dimensional arrays, it is important to have a mental model to think them as collection of arrays.

Hope this article ease some pain for those who are learning Machine Learning and struggle to understand the dimensionality of the arrays!

Reference

• NumPy Official Documentation: https://numpy.org/devdocs/user/absolute_beginners.html#array-fundamentals