But when a genius arises in art, it outlasts the ages; when such a moment occurs, it creates a decision for decades and centuries.

Stellar Moments of Humankind – Stefan Zweig

An A/B Testing in 1920s that changed the world

“I believe tea tased different depending upon whether the tea was poured into milk first, or milk was poured into milk first”, said a women in a group of University fellows and their wives, in a sunny afternoon in Cambridge, England in 1920s.

A debate was started between the scientific minds of statisticians.

It was a century ago, when science began to evolve from clockwork universe, where there was a belief in Science that things happen in deterministic way, to a new paradigm – the statistical model of the world. Scientists started to study the data from observations and experiments, and to derive new knowledge from them. Concepts such as probabilities, randomness, and chances started to evolve, and scientific experiments became more robust under these new beliefs and methodologies.

“Let’s test this hypothesis”, said the man with the Vandyke beard, whose name is Ronald Fisher. (He would later be knighted Sir Ronald Fisher).

The hypothesis

As with all the A/B testing scenarios, we first have to lay down our hypothesis.

• Null Hypothesis: There is no difference between pouring milk first or tea first to make a tea
• Alternative Hypothesis: There is a difference between them.

Fisher’s idea is simple. Under a randomised samples of tea, if the lady can guess correctly of all these samples which are poured with milk first and which are the otherwise, then it can be said that there is a significant difference between them.

The only thing that he wants to avoid, as in all other experiment settings, is the lady can “guess” all cups of tea correct by “chance”. As a statistician, he proposed a robust method to do this experiment, which is later documented in his book “Statistical Methods for Research Workers”.

Designing the experiment

Fisher designed the experiments with 8 cups of tea, 4 of which were poured in milk first, and 4 of which were poured with tea first. These cups of teas were randomised (in a way where there was no human intervention, such as by using dice, cards, etc). He then asked the lady (the subject) to taste the tea, and see if she could guess it right.

The selection of 8 cups of tea is a calculated choice. Since there are 4 cups of each kind of tea, there are 70 combinations.

If the lady can guess all cups of tea correct, the chance would be chance. That is a very small chance if one can guess it all correct, even though there is no difference in the tea.

The test of significance

For those who are more familiar with statistics would recognise that 1.4% chance of “guessing it right even though there is no difference in the tea”, is the p-value of the modern world. By definition, p-value is the chance of seeing the observation, given the null hypothesis is true.

In this case, since the order of the 8 cups of tea are randomised, if the lady can randomly guess correctly which 4 cups are poured with milk first, and which 4 are otherwise, the chance is only 1.4%. Unless, there is a difference between them, which leads to a rejection of the null hypothesis.

Clearly, in the Lady Tea Tasting case, the chance of guessing all right is 1.4%, less than 5%. In modern statistics, we will reject the null hypothesis

The 5% threshold

However, as also mentioned in Fisher’s book “The Design of Experiments”, the selection of 5% threshold is more or less a convenient choice.

It is usual and convenient for experimenters to take 5 per cent, as a standard level of significnce, in the sense that they are prepared to ignore all results which fail to reach this standard, and by this means, to eliminate from further discussion the greater part of the fluctuations which chance cuases have introduced into their experimental results.

The design of experiments 7th edition, pp.13, Sir Ronald A. Fisher

However, in the book, he also discussed the scenarios where the lady make 3 right guesses and 1 wrong guess. By mathematical permutation, there will be 16 scenarios where one will get 3 right guesses and 1 wrong from 70 combinations, which makes it chance. Should we still take that?

Fisher suggested that although the result is biased to the positive side, it could not be judged as statistically significant of a real sensory discrimination.

The rare case of 3 right and 1 wrong could not be judged significant merely because it was rare, seeing that a higher degree of success would frequently have been scored by mere chance.

The design of experiments 7th edition, pp.15, Sir Ronald A. Fisher

How larger sample size can help?

As we see the whole discussion of hypothesis testing is around whether the difference is due to “chance”, having a larger sample size can help to reduce the sampling error.

Considering the same tea tasting case, and further imagine there are 2 scenarios. The first scenario is having a set of 6 cups of tea, in which there are 3 of both kinds; and the second scenario is having a set of 10 cups of tea, in which there are 5 of both kinds.

Scenario 1:

• There will be 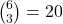combinations. The chance of guessing all correct is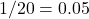

Scenario 2:

• There will be 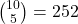combinations. The chance of guessing all correct is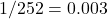
• There will be 25 combinations of selecting 1 wrong, making up to 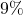chance, which is a lot less than 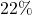in the case of 8 sets.

Learnings

The world of statistics have changed a lot since then, with the contribution of Sir Fisher and a lot of great minds. It also shapes the Data Science field today.

For those who are interested more in this story, I highly recommend the book The Lady Tasting Tea How Statistics Revolutionized Science in the Twentieth Century by David Salsburg, PhD! (I am not an affiliate)

For those who may interested in the result, she clear the tests and chose all cups of tea correctly, by the way. (As reported by Dr. Salsburg in his book)

References

• The Lady Tasting Tea How Statistics Revolutionized Science in the Twentieth Century (David Salsburg, PhD)
• The Design of Experiments (Sir Ronald A. Fisher)